Есть ли шансы у аксиоматического дедуктивного метода в теории музыки?

[combinare]

звуковысотный класс,питч - тембронезависим,он- частота синусоидальной волны

Human perception of musical intervals is approximately logarithmic with respect to fundamental frequency: the perceived interval between the pitches "A220" and "A440" is the same as the perceived interval between the pitches A440 and A880. Motivated by this logarithmic perception, music theorists sometimes represent pitches using a numerical scale based on the logarithm of fundamental frequency. For example, one can adopt the widely used MIDI standard to map fundamental frequency, f, to a real number, p, as follows
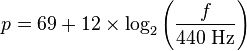This creates a linear pitch space in which octaves have size 12, semitones (the distance between adjacent keys on the piano keyboard) have size 1, and A440 is assigned the number 69.

[vcirkov]

Но́та (лат. nōta — «знак», «метка») в музыке — это графическое обозначение звука музыкального произведения, один из основных символов современной музыкальной нотации.

Не верю своим глазам. Вы одной только ссылкой заставили усомниться комматора в том, что нота и звук тождественны. Я же потратил безрезультатно на это несколько лет.

[commator]

звуковысотный класс,питч - тембронезависим,

Здесь не всё просто.

Из-за нелинейности слуха есть субъективные гармоники и может быть какая-то малоподвижная субъективная форманта, относительно которой звуковысотность каждой синусоиды обязана иметь собственную распознаваемую тембровую помеху, совпадающую с такой же тембровой помехой в составе, например, каждого пилообразного сигнала соответствующей звуковысотности.

Ув. murom эти субъективные тембровые помехи легко выделяет из звуковысотностей любого тембра и вместе с ощущением высоты распознаёт имя музыкальной ноты.

Как-то само собой получилось назвать уровень музыкальной ноты звуковысотностью. Может быть пользоваться словом звуковысотность для того, что отображает музыкальная нота?

[combinare]

Здесь не всё просто.

Ув. murom эти субъективные тембровые помехи легко выделяет из звуковысотностей любого тембра и по ним уточняет уровень высоты.

Как-то само собой получилось назвать уровень музыкальной ноты звуковысотностью. Может быть пользоваться словом звуковысотность для того, что отображает музыкальная нота?

Не уверен,что стоит принимать на веру мнение Уважаемого murom'а.
в одной книжке про Алису написано,что люди,проживающие в Австралии,именуются антиподами,потому как ходят они вверх ногами и вниз головой.

[commator]

Не уверен,что стоит принимать на веру мнение Уважаемого murom'а.

Спросил об этом у супруги и она ответила, что абсолютисты железно пользуются способностью распознавать имена нот через ощущения одинаковых тембровых особенностей, которые присутствуют в одинаковых звуковысотностях разных тембров.

Ещё и это вспомнил:

Для тех, кто его никогда не ощущал и вообще понятия не имеет, о чем речь, предлагаю следующий эксперимент. Если есть возможность, возьмите источник звука, который мог бы дать ровный, неменяющийся, достаточно громкий звук. Я использую для этого основной тон электрооргана, но подойдет и синтезатор, или осциллограф. Звук должен быть достаточно громким, но не оглушительным. Нажмите ноту си первой октавы. Прислушайтесь к физическому ощущению, возникающему внутри уха. Покрутите головой, оно должно слегка меняться. Это ощущение имеет похожий характер с тем, как закладывает уши в самолете. Это не шутка.

Затем, наслушавшись си, возьмите ля-бемоль. С тех же позиций послушайте его. Покрутите головой. Сравните с ощущением си.

Прочитайте этот абзац после того, как выполнили задание.

Большинство из тех, кому я это предлагал, ощущали си как более резкое, пронзительное, а ля-бемоль, как более мягкое, широкое.

Каков Ваш опыт?

2. Второй критерий - это обертоновый состав. Это очень хорошо слышно на ф-п, но относится ко всем музыкальным звуками. Дело в том, что все музыкальные звуки обладают обертоновым рядом. Если вы возьмете на ф-п какую-нибудь ноту в среднем регистре и послушаете ее 5-10 секунд КАК РАЗВОРАЧИВАЮЩИЙСЯ ПРОЦЕСС, вы можете пронаблюдать характерное звучание каждой ноты, субъективно оно будет напоминать что-то вроде "у-а-у" или "э-уэ", причем имеющее такой "волнообразный" характер. Это вызвано именно тем, что струна колеблется одновременно и целиком, и частями. Опять же ноты имеют разные частоты, поэтому этот волнообразный процесс разворачивается с разной скоростью. Кроме того каждая нота звучит по-своему, этот ее "внутренний процесс" отличается от внутреннего процесса другой ноты. Если у вас развито внимание к мелким деталям, вы это несомненно заметите. Только не слушайте на расстроенном ф-п!

На других инструментах это не так слышно, однако даже при прослушивании звука осциллографа без обертонов, человеческое ухо эти обертоны генерирует само (в среднем ухе) и все равно воспринимает движение обертонов.

У аболютников с рождения вся эта беда просто не осознается, процесс распознавания происходит мгновенно, однако они не могут сказать, почему)

[murom]

Не уверен,что стоит принимать на веру мнение Уважаемого murom'а.
в одной книжке про Алису написано,что люди,проживающие в Австралии,именуются антиподами,потому как ходят они вверх ногами и вниз головой.

Я прибыл в Австралию, когда мне было 42 года. А абсолютный тембровый слух у меня сильно проявился еще в школьные годы.
А тембр даже от синусоиды тоже слышен разный. Мне кажется, что это можно объяснить особенностями нашей физиологии, анатомии и пр. нелинейными искажениями по пути из уха в мозг. Но меня это не интересует, меня интересует только определении высоты тона на слух. Бывают такие тембры музыкальных инструментов, которые меня путают (я уже писал о гобое), и это говорит только о том, что у меня не высотный абсолютный слух (он точно определяет при любых условиях), а именно тембровый (могу ошибиться, если играет необычный для меня инструмент, когда я не слышу особенности каждой ноты из-за специфики тембра этого инструмента.) Но если мне привыкнуть к этому новому инструменту, то и его звуки начну определять правильно.

[combinare]

меня интересует только определение высоты тона на слух. Бывают такие тембры музыкальных инструментов, которые меня путают (я уже писал о гобое), и это говорит только о том, что у меня не высотный абсолютный слух (он точно определяет при любых условиях), а именно тембровый (могу ошибиться, если играет необычный для меня инструмент, когда я не слышу особенности каждой ноты из-за специфики тембра этого инструмента.) Но если мне привыкнуть к этому новому инструменту, то и его звуки начну определять правильно.

Множество программ (pitch - to - midi) безошибочно справляются с определением высоты тона ,
интересно,насколько правильно Вы берете на инструменте слышимую внутренним слухом звуковысотность,-
ведь в этом случае тембр или форманта не зависит от конструкции инструмента,не правда ли?

[commator]

Не верю своим глазам. Вы одной только ссылкой заставили усомниться комматора в том, что нота и звук тождественны. Я же потратил безрезультатно на это несколько лет.

Может быть укажете на подтверждения Вами высказанного?

[lerit]

Может быть укажете на подтверждения Вами высказанного?

Это и я могу:

Как же наилучшим образом называть одним словом звук, отображаемый музыкальной нотой?

Как-то само собой получилось назвать уровень музыкальной ноты звуковысотностью. Может быть пользоваться словом звуковысотность для того, что отображает музыкальная нота?

[commator]

для существования некоторой аксиомы о равенстве двух нот, без которой не может быть шансов у аксиоматического дедуктивного метода в теории музыки.

Предлагаю такую аксиому:

Всеми одинаково ощущаемые звуковысотности считаются равными.