-
30.10.2011, 17:20 #11
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Пришпилил решётку другим способом. Может быть теперь отобразится, и Вы сами всё увидите. Для выяснения сути эйлерова описания, ешё раз даю ссылку на От себя скажу, что скромный Эйлер по сути был первым, кто дал эту наглядную и всё ещё актуальную схему квинто-терцовой организации октавных классов высот. Негоже его имя затирать чьими-то другими. Особенно именами тех, кто так или иначе воспользовался сутью решётки Эйлера.
Последний раз редактировалось commator; 01.11.2011 в 11:21.


- Регистрация
- 04.06.2008
- Адрес
- Минск
- Сообщений
- 1,712
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Оголевец всегда интерпретировал “правильную” орфографию хроматической гаммы (приведенную в цитированном выше фрагменте также у Холопова) только в Пифагоровом строе. Но были попытки ее интерпретации также и в “чистом строе”; одну из таких попыток (очень критически!) разбирает Оголевец:


- Регистрация
- 04.06.2008
- Адрес
- Минск
- Сообщений
- 1,712
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
У меня вопрос: нельзя ли представить обсуждаемые вами ЧИПы в аналогии со стереометрией? Например, трехмерность - наиболее привычная для восприятия - это какой предел? ЧИП1 - это будет, вероятно, точка или один звук, а ЧИП2 - одна линия или октава? Это мне понятно, но здесь нет полного строя. Я не собираюсь переводить музыку на визуальный язык, просто хочется разобраться, почему полная система ПС связывается с ЧИП3? Видимо, это можно уже связать с объемом трехмерного пространства, в котором все измеряется значениями векторов?
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
:
<<Гармонические решетчатые схемы Джо Монзо
Текст и схемы © 1998 Джозеф Л. Монзо
Самый лучший способ, который я открыл, чтобы понять так много гармонической информации, сколь возможно в чисто-интонационной системе музыкальной настройки, есть использование решетчатых схем, которые изображают высоты как связанные векторами точки в многомерном пространстве.
В чисто-интонационной системе музыкальной настройки каждая нота представляет собой соотношение, которое описывает родство ноты с другой нотой, как правило, той, что используется в качестве основы для системы в целом. Этот основной тон имеет соотношение 1/1, также описываемое как 1:1 или 1 к 1.
Любое число может быть разложено в ряд простых чисел, каждое из которых представляет собой основание, у которого есть показатель, являющийся положительным или отрицательным, представляя числа > 1 или < 1 соответственно, вне показателя = 0, что представляет 1, одинаковость в умножении.
Степени 2 все гармонически равноценны этой одинаковости 1, таким образом, степени 2 представляют собой "октавы", и поэтому не имеют отчётливого влияния на гармонии, и могут быть устранены, исключая "октавную" регистровку под особым рассмотрением. Таким образом, схемы обычно начинают с простого основания 3.
Мои решетчатые схемы толкуют каждое простое основание, как неповторяемое измерение в пространстве, со всеми показателями расходящимися лучами наружу от центрального 1/1, что соответствует всем числам в 0-й степени или n0.
Рассматриваемые в 2-мерном пространстве векторы, что соединяют каждый показатель перемещаются в неповторяемом направление для каждого простого числа. Это направление определяется углом, который представляет величину в центах (внутри «октавы») этого простого числа в 1-й степени, начиная с позиции 6 часов.
Так 31, что есть сотношение 3/2 и 702 цента, имеет вектор, исходящий от 1/1 в непосредственной близости от позиции 1 час (потому что 6 + 7 mod 12 = 1).
51, что есть сотношением 5/4 и 386 центов, имеет вектор, исходящий в позиции чуть менее 10 часов (6 + 3,86 = 9,86), и так далее.
Отрицательные показатели просто излучаются наружу с противоположной стороны.
Векторы также различаются по длине и толщине соответствуя простым основаниям с ними соединёнными, с 3 кратчайшие и толстейшие.
Интересно, что даже несмотря на 2-мерное пространство бывшее средой, в которой эти измерения были сделаны, они кажутся глазам образующими 3- или даже более -мерные построения, несколько напоминающие кристаллы.
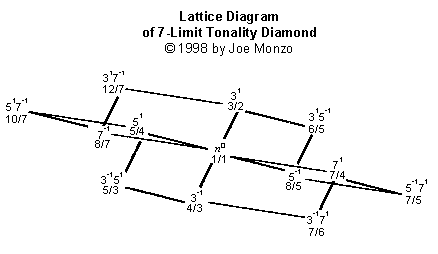
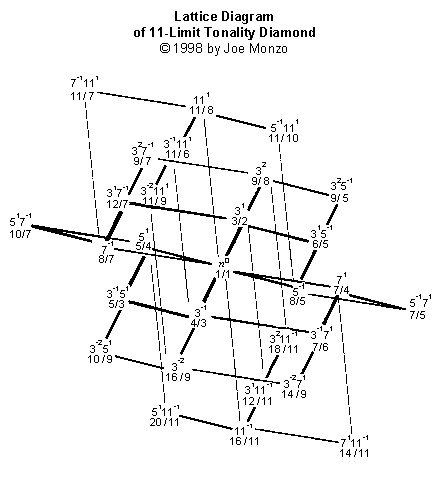
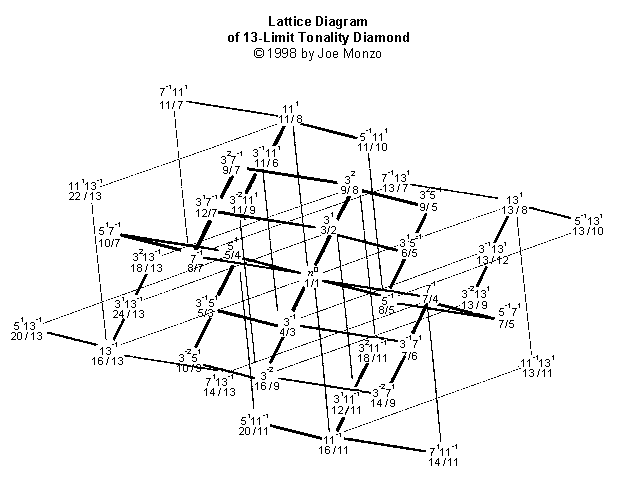
Гарри Парч изобрёл построение, им названное "тональностный ромб". Оно показывает все гармонические родства соотношений с номерами под определенным "нечётным пределом" (исключая "октавное удвоение", или умножение на 2, которое он использовал, чтобы держать каждое соотношение в той же "октаве", что и в наиболее обычных исходных скалах).
Эти "ромбы", которые просто становятся больше и содержат экспоненциально больше соотношений с каждым новым дальнейшим нечетным пределом по версии Парча, принимают совершенно другой вид, когда иллюстрированы используя мои решетки. Процесс, конечно, обращается к моим художественным чувствам.
Я иллюстрирую здесь «тональностные ромбы» предела 5, предела 7, предела 9, предела 11, и предела 13, как представленные моими решетчатыми схемами.
Симметрия, которую Парч отметил в своих скалах и тональностных ромбах, является легко видимой здесь, хотя тональностные ромбы в этом представлении не вполне симметричны, как в некоторых других системах, что я разработал
...
...
...
...
...>>
Пифагорейской предела 3 решётки нет в помине. Не потому ли, что её ромб до тональностного не дотягивает?
Ведь для ощущения тональности нужны терции, причём достаточно явно ощущаемые первыми из натуральных, что между обертонами/унтертонами 4, 5 и 6. Пифагорейские же терзают слух фальшивя где-то на задворках натуральных скал между номерами 64, 81 и 96.
Последний раз редактировалось commator; 10.08.2012 в 11:17.
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Спасибо за труд, очень интересно. Здесь все о нем:
Думаю, нужно рассказать предысторию моего интереса к объемному восприятию гармонии. Ранее думал о том, что трезвучие - имитация трехмерности в двухмерном пространстве. Полный аккорд с возможностью аккордового голосоведения за счет переходов на осях общих звуков уже не имитация, а реальный объем в восприятии. Ну, и представлялись какие-то объемные треугольники. Понять же как совместить качество целого числа три с четырьмя вершинами и привести аналогию в полное соответствие сложно. Попытаюсь разобраться с решетками, но пока закончу свой рассказ. Захотелось мне нарисовать дачный дом с оригинальной конструкцией (два пересеченных куба). Пришлось скачать простую программу 3D-моделироания. Очень увлекся этой игрушкой и обнаружил, что стал петь в ЧС, причем, ощущая реально объемы аккордов, в которых звуки сходятся, когда все интонируют чисто. При таком интонировании возникает ощущение, аналогичное тому, как в программе, когда тот или иной вектор высвечивается цветом при правильном ведении линии.
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Не совсем понятно, как все же правильно это называть. Ведь речь идет не столько об интонации, а о ЧС со всеми его проблемами. Схему ЧС можно рассматривать базовой моделью для интонирования, но называть строй интонированием не очень правильно. Возможно, эта оговорка не принципиальна, но все же...
Его можно послушать здесь:"Гарри Парч изобрёл построение, им названное "тональностный ромб". Оно показывает все гармонические родства соотношений с номерами под определенным "нечётным пределом".
Характерно то, что в поисках микротональных моделей звукорядов он приблизился к звучанию фольклора. Сам же фольклор по прежнему в этом смысле никому не интересен.
Это-то мне и было не понятно в ЧИПах. Как можно терцию ПС считать полноценным звеном акустического строя? В данном случае не о выразительности речь, поскольку высокая терция может быть представлена в любом положении от темперированной и выше. Тем более, как Вы утверждаете, что
Пифагорейской предела 3 решётки нет в помине. Не потому ли, что её ромб до тональностного не дотягивает?Я бы не стал это тесно связывать с тональностью. Пока у меня сложилось такая конструкция для простых гарм. функций: Предел 2 (октава) - это основная ось (пусть это будет тональностью, если Вам угодно). На ней возникает точка, которая делит октаву, - это ПИЧ3. Этот звук мы делаем второй осью, поскольку он характеризует другое качество целого числа. Ограничивая длину этой второй оси, мы должны показать уже другое построение на этой оси, которое будет соответствовать терции, иначе 5-му пределу. На этом уровне можно остановиться, то есть не рисовать следующую ось, а ограничиться только точкой, которая закроет треугольник. Такое же построение можно сделать относительно доминанты и прочих функций. Треугольники соединяются дополнительными линиями в местах удвоения звуков, что и дает ощущение объема.для ощущения тональности нужны терции, причём достаточно явно ощущаемые первыми из натуральных, что между обертонами/унтертонами 4, 5 и 6. Пифагорейские же терзают слух фальшивя где-то на задворках натуральных скал между номерами 64, 81 и 96.
Последний раз редактировалось vcirkov; 30.07.2012 в 12:38.



- Регистрация
- 22.01.2009
- Сообщений
- 2,190
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Бред какой-то….
Допустим в консонансовой композиции сто нот “фа”.
И каждый раз опытный музыкант воспроизводит их с разной центностью,интервально подстраиваясь….
Транспонируем тональность этой композиции и сто “фа” качнутся в другую разноцентность…
Какая тут система?
Амбюшюра в мундштуке,воздушного посыла на голосовые связки,микропозиции смычка разве для этого мало…?
"Фальшивость" хроматизма родила самое главное в музыке-артикуляционную и интонационную фантазийность,непохожесть и узнаваемость музыкантов.
А при диссонансовой гармонизации современное расположение тонов через сто центов вообще есть благо.
Некое созвучие через тон (из модального гексахорда) требует равной стоцентности,отвергая логику "cистемы чистой интонации" напрочь,раскрепощая границы допустимой центности солиста по-холоповски …
«Система»-это когда универсально для всей классической музыки,для всех её гармонических предпочтений.
Когда этого нет-это сектантский бред,изобретение "пятого колеса".
Последний раз редактировалось wau2009; 30.07.2012 в 13:45.
 Re: Система чистой интонации предела 5
Re: Система чистой интонации предела 5
Похожие темы
-
Определение интонации и музыки
от Muzylo в разделе Философия и музыкаОтветов: 374Последнее сообщение: 23.10.2016, 22:17 -
Корректные MIDI-модели для систем Чистой Интонации
от Математик в разделе Теория музыкиОтветов: 83Последнее сообщение: 09.07.2015, 22:12 -
Система чистой интонации предела 7
от Математик в разделе Теория музыкиОтветов: 150Последнее сообщение: 20.02.2015, 14:04 -
Мигрирующие интонации
от Джованни Аллегри в разделе БеседкаОтветов: 0Последнее сообщение: 03.05.2012, 12:57 -
Немного рекламы в чистой воде...
от Romka в разделе СмешноОтветов: 5Последнее сообщение: 26.09.2011, 14:02








 Ответить с цитированием
Ответить с цитированием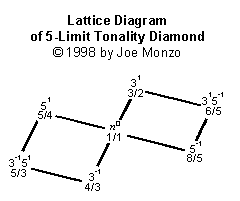






Социальные закладки